风机控制 - PID

1. PID概述

PID控制算法是结合比例、积分和微分三种环节于一体的控制算法。

PID控制的实质就是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出。

1.1 连续控制系统中的理想PID控制规律

$$
u(t) = K_p\left{e(t) \quad + \quad \frac{1}{Tt}\int{0}^{t}{e(t)dt} \quad + \quad T_D\frac{de(t)}{dt}\right}
$$

$$
K_p - 比例增益
$$

$$
T_t - 积分时间常数
$$

$$
T_d - 微分时间常数
$$

$$
u(t) - PID控制器的输出信号
$$

$$
e(t) - 给定值r(t)与测量值之差
$$

1.2 PID控制原理

==闭环控制==是根据控制对象输出反馈来进行校正的控制方式，它是在测量出实际与计划发生偏差时，按定额或标准来进行纠正的。比如控制一个电机的转速，就得有一个测量转速的传感器，并将结果反馈到控制路线上。提到闭环控制算法，不得不提PID，它是闭环控制算法中最简单的一种。PID是比例 (Proportion) 、积分 (Integral) 、微分 (Differential coefficient) 的缩写，分别代表了三种控制算法。通过这三个算法的组合可有效地纠正被控制对象的偏差，从而使其达到一个稳定的状态。

1.3 PID图解

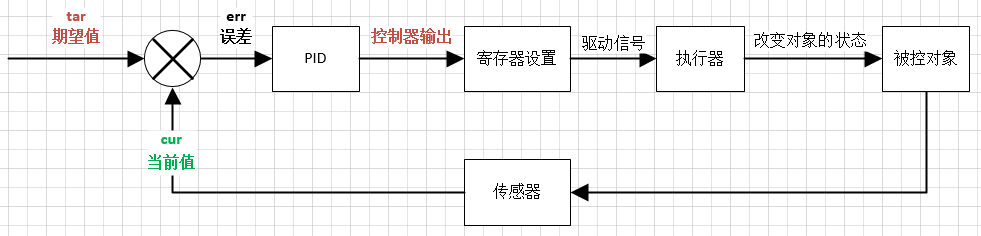
1.4 常用PID算法

1.4.1 PI算法

特点：

• 从时域上看，只要存在偏差，积分就会不停对偏差积累，因此稳态时误差一定为零。
• 不足：比例与积分动作都是对过去控制误差进行操作，不对未来控制误差进行预测，限制了控制性能。
• PI调节将比例调节的快速反应与积分调节消除静差的特点结合，实现好的调节效果。
• PI调节适用于控制通道滞后较小、负荷变化不大、工艺参数不允许有静差的系统。

1.4.2 PD算法

适用于舵机快速响应。对于惯性较大的对象，常常希望能加快控制速度，此时可增加微分作用。

特点：

• 比例控制对于惯性较大对象，控制过程缓慢，控制品质不佳。比例微分控制可提高控制速度，对惯性较大对象，可改善控制质量，减小偏差，缩短控制时间。
• 理想微分作用持续时间太短， 执行器来不及响应。实际使用中，一般加以惯性延迟，称为实际微分。
• PD 调节以比例调节为主，微分调节为辅，PD调节是有差调节。
• PD 调节具有提高系统稳定性、抑制过渡过程最大动态偏差的作用。
• PD 调节有利于提高系统响应速度。
• PD 调节抗干扰能力差，一般只能应用于被调参数 变化平稳的生产过程。
• 微分作用太强时，容易造成系统振荡。

1.4.3 PID算法

将比例、积分、微分三种调节规律结合在一起， 只要三项作用的强度配合适当，既能快速调节，又能消除余差，可得到满意的控制效果。

特点：

• PID 控制作用中，比例作用是基础控制；微分作用是 用于加快系统控制速度；积分作用是用于消除静差。
• 只要比例、积分、微分三种控制规律强度配合适当， 既能快速调节，又能消除余差，可得到满意控制效果。
• Kp 较小时，系统对微分和积分环节的引入较为敏感，积分会引起超调，微分可能会引起振荡，而振荡剧烈的时候超调也会增加。
• Kp 增大时，积分环节由于滞后产生的超调逐渐减小，此时如果想要继续减少超调可以适当引入微分环节。继续增大 Kp 系统可能会不太稳定，因此在增加 Kp 的同时引入 Kd 减小超调，可以保证在 Kp 不是很大的情况下也能取得较好的稳态特性和动态性能。
• Kp 较小时，积分环节不宜过大，Kp 较大时积分环节也不宜过小（否则调节时间会非常地长），当使用分段PID ，在恰当的条件下分离积分，可以取得更好的控制效果。原因在于在稳态误差即将满足要求时，消除了系统的滞后。因此系统超调会明显减少。

1.4.4 位置型PID和增量型PID的比较：

• 位置式需引入初始阀位值，增量式不需要。
• 位置式需防积分饱和，增量式不会产生积分饱和。
• 只有存在偏差时，增量式才会有输出。
• 增量式容易实现从手动到自动的切换。
• 位置式PID控制的输出与整个过去的状态有关，用到了误差的累加值;而增量式PID的输出只与当前拍和前两拍的误差有关，因此位置式PID控制的累积误差相对更大。

优点：

• 算式中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果。
• 计算机每次只输出控制增量，即对应执行机构位置的变化量，故机器发生故障时影响范围小、不会严重影响生产过程。
• 手动—自动切换时冲击小。当控制从手动向自动切换时，可以作到无扰动切换。

缺点：

• 需要对控制量进行记忆。
• 存在稳态误差。

1.4.5 PID优化方法

①抗积分饱和：

如果系统总是存在统一的方向偏差，就可能无限累加而进行饱和，极大影响系统性能。

所谓积分饱和就是指系统存在一个方向的偏差，PID控制器的输出由于积分作用的不断累加而扩大，从而导致控制器输出不断增大超出正常范围进入饱和区。当系统出现反响的偏差时，需要首先从饱和区退出，而不能对反向的偏差进行快速的响应。

为了解决积分饱和的问题，人们引入了抗积分饱和的PID算法。所谓抗积分饱和算法，其思路是在计算U(k)的时候，先判断上一时刻的控制量U(k-1)是否已经超出了限制范围。若U(k-1)>Umax，则只累加负偏差；若U(k-1)<Umin，则只累加正偏差。从而避免控制量长时间停留在饱和区。

几种我能看懂的方法：

• 在饱和的时候将积分器的累计值初始化到一个比较理想的值。
• 若积分饱和因为目标值突然变化而产生，将目标值以适当斜率的斜坡变化可避免此情形。
• 将积分累计量限制上下限，避免积分累计量超过限制值。
• 如果PID输出已经饱和，重新计算积分累计量，使输出恰好为合理的范围。

系统对于积分项的要求是，系统偏差大时，积分作用应该减弱甚至是全无，而在偏差小时，则应该加强。积分系数取大了会产生超调，甚至积分饱和，取小了又不能短时间内消除静差。因此，根据系统的偏差大小改变积分速度是有必要的。 变积分PID的基本思想是设法改变积分项的累加速度，使其与偏差大小相对应：偏差越大，积分越慢; 偏差越小，积分越快。

②串级PID：

类比于小车上坡，因为单环PID输出的速度 V 不一定是真实的速度 V，所以内环再加上速度环PID，构成串级PID（外环为位置环，输出的值是小车的理论速度，内环为速度环，输入是小车的理论速度，希望尽可能的使输出为理论速度），外环的输出是内环的输入。

同样类比于四轴，外环为角度环，输出的是期望达到该角度所需要的PWM（也就是角速度，也可以理解为角速度和PWM的映射），内环为角速度环，输入是期望的角速度和自身真实的角速度，输出为最终的PWM（角速度）。

串级PID可增加系统的稳定性，抗干扰。

为什么外环的输入是内环的期望呢？因为你在设计控制器的时候，内环的目的就是实现用执行器控制直接能改变的变化量，外环的目的就是找到合适的曲线，来引导目标的微分变化，从而达到间接控制的效果。

为什么要用串级PID呢？

看上去PID不是已经够完美了吗？只要我能给出反馈，我就能控制所以的物理量不是吗？

为什么还要双闭环PID呢？那为什么说外环输入是内环期望呢？为什么位置误差经过PID就变成速度期望了呢？

那我们就来设计一个位置控制器吧！

感觉好像没什么问题，但是跟之前有些许不一样，之前我们的「执行器能直接改变反馈值」，但是在这个控制器里，执行器依然只能改变升力，只不过，因为升力改变，会有加速度，从而导致速度变化，最终导致位置变化。

如果你按照图中的思路设计控制器，那就说明「你只对位置有期望」，这意味着你对升力，速度没有期望，也就意味着加速度，速度是什么都无所谓。

所以实际效果变成什么呢？

你会以一个你无所谓的加速度，和速度，到达你的期望位置。

这时候奇怪的事情发生了，到达你的期望位置时有加速度和速度，那这个就不是「到达期望位置」了，这叫「经过期望位置」。你会发现你的对象在期望位置附近“反复横跳”，超过后，又退回去，退过了，又超过去。

这时候你才想起来，原来「你期望的是停在期望位置上」。

什么叫停在期望位置上？

就是到达期望位置的同时加速度与速度都为0。

这个问题是如何产生的，为什么之前没有这个问题？

之前在单级PID时我们举的例子中，期望被控制的物理量，都是可以直接被执行器改变的。

但是在这个例子中，期望被控制的物理量，不能被执行器直接改变，但是可以被间接改变，并且你知道间接改变的过程。

之前我们想控制位置，类似于控制机器人，给出命令，它直接走到对应的位置。

现在我们想控制位置，类似于控制车，你只能踩油门加速，或者刹车进行减速，你只能通过速度控制间接控制位置。

但是你肯定知道，车我们也是可以控制位置的，还记得驾校里的倒车入库吗？不就是让你精准的控制位置吗？

开车的时候是怎么控制位置的呢？你想停在指定位置的时候，你先以一定的速度前往指定位置，快到的时候，通过刹车不断减速，直到速度为0，停到期望的位置。

这个过程告诉了我们什么？我们只通过控制速度就可以间接控制位置，也就是说我们可以通过控制某个物理量的变化快慢，从而间接控制这个物理量。

所以我们只需要选择合适的速度变化曲线就可以停在我们想要的位置。那我们就可以把控制器设置成下面的结构。

什么是合适的速度变化曲线呢？

首先当到达期望位置的时候，速度应该为0。其次当没有到达期望位置的时候，期望速度是可以减小位置误差的。

总结一下：

期望速度必须能减小位置误差，且位置误差为0时，期望速度为0。

什么意思呢？

如果前方为正方向，当期望位置在我们前方时，即 target-current>0，那我们就希望能有个向前的正速度，去缩小这个误差，当误差为0时，我们希望速度为0。满足这样的过程的速度变化曲线，就是合适的速度变化曲线。

想想开车的时候，快到终点的时候会出现什么操作？

新手在没达位置的时候，希望有一个比较快的速度，快到了直接一脚刹车踩到底。高手可以提前预判，匀速降低速度。

更高阶的可以变化的减速让整个速度变化如丝般顺滑。

就有了下面的曲线。

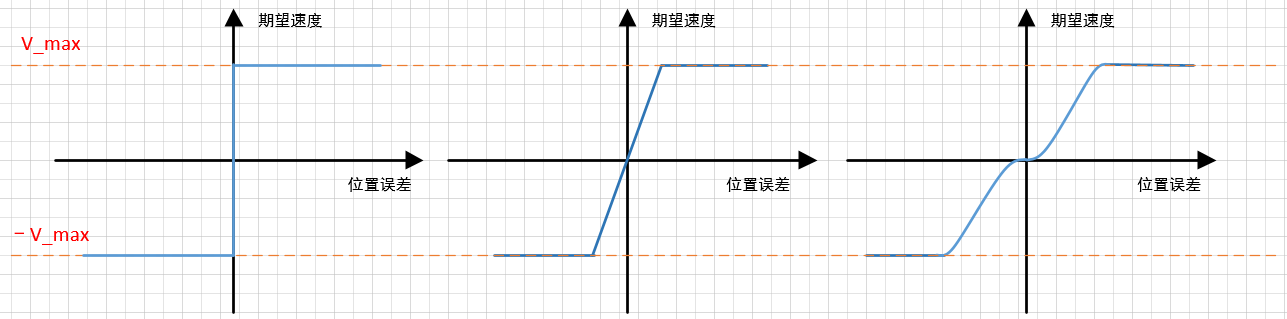
因为我们对期望速度的要求：

期望速度必须能减小位置误差，且位置误差为0时，期望速度为0。所以我们发现这些期望速度都是与位置误差相关的且经过0点的曲线。

位置误差与期望速度在这时候才建立起的关系，注意，强调一遍，是我们主动把位置误差与期望速度联系起来的，起因是我们希望控制速度达到控制位置的效果。

而这种控制能够被实现的本质是：

速度与位置存在我们已知的简单变化关系，即速度的积分是位置，所以改变期望速度才能改变位置，才能减小误差。

所以合理的控制过程应该就可以设计成这样。

只要找个合适的函数，根据误差生成合适的期望速度曲线就可以了。

我们最常使用的是什么样的曲线呢？

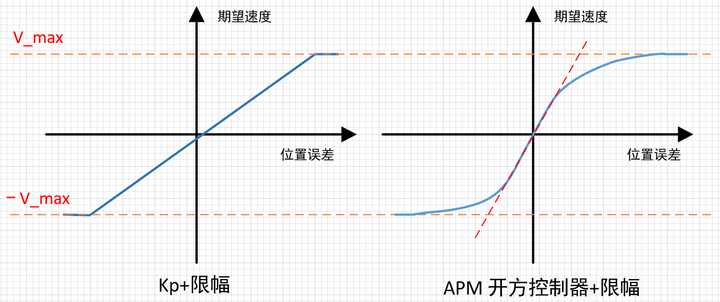
只要是满足合适的期望速度的曲线都可以作为期望速度，显然如果在外环使用PID也是可以的，但是为什么实际中不这么用呢？因为添加积分(I)后，导致响应变慢，添加微分(D)容易引入噪声，只用P又简单又有效，何乐而不为呢？

到这里外环的输出终于理所应当的变成了内环的期望，但是这并不是因为这件事本就应该成立，而是通过你的设计，和真实存在的物理关系，才设计出来的合情合理的双闭环控制器。

设计过程：

1. 执行器输出无法直接控制目标物理量。
2. 发现控制器能控制物理量的变化量(微分)。
3. 你想了个办法，可以通过控制物理量的微分，按照某种曲线变化，从而达到间接控制目标物理量。
4. 这个曲线必须满足两点，存在目标物理量误差的时候，应该产生因一个能减小这个误差的变化，且当没有误差的时候，变化量也应该为0。
5. 选择最简单实用的曲线即可，所以外环选择KP。
6. 间接控制能成功的原因是因为，执行器能改变的量，与目标物理量之间有简单的物理关系。

所以为什么外环的输入是内环的期望呢？因为你在设计控制器的时候，内环的目的就是实现用执行器控制直接能改变的变化量，外环的目的就是找到合适的曲线，来引导目标的微分变化，从而达到间接控制的效果。